Encontrar as tensões e deformações de estruturas submetidas a determinadas cargas é uma importante atividade de engenharia. Essa tarefa já apresenta suas complicações quando as estruturas são construídas com materiais isotrópicos, onde todas as propriedades dos materiais não variam com a direção, e com geometrias simples. Agora quando se trata de um barco construído com painéis sandwich onde as faces são construídas em laminado sólido e o núcleo é de espuma, o processo se torna um pouco mais difícil.
Além disto, os esforços na estrutura de um barco, seja a vela ou a motor, são extremamente complexos e variam constantemente de intensidade e direção. Embora o método dos elementos finitos não ofereça uma solução precisa, ele fornece uma boa aproximação dos valores de tensão e deformação em cada parte da estrutura possibilitando ao projetista ou construtor otimizar a quantidade de materiais além da direção dos reforços.

O princípio das estruturas sandwich é que os esforços de tração e compressão são suportados pelas faces enquanto o material de núcleo suporta os esforços de cisalhamento. A maneira mais eficiente de estudar como um painel desse tipo se comporta com diferentes condições de contorno e diferentes condições de carga é por meio do método de elementos finitos, um procedimento numérico que divide as partes da estrutura em pequenos elementos de comportamento conhecido. A análise dos valores de tensão e deformação da estrutura é feita através da solução de uma equação matricial que segue o principio da Lei de Hooke, que diz que as tensões são proporcionais às deformações.

Algumas hipóteses devem ser levadas em consideração para utilizar o método de elementos finitos para prever o comportamento de estruturas sandwich, sendo que a primeira é que as tensões perpendiculares ao plano do painel são negligenciáveis tanto no núcleo quanto nas faces. A segunda é que o módulo de elasticidade do núcleo é tão baixo que a rigidez à flexão é fornecida apenas pelas faces. Além disso, os deslocamentos deve ser pequenos, fazendo com que a teoria de flexão seja válida. Por fim, as faces devem ter baixa espessura quando compradas ao núcleo, o que significa que a rigidez à flexão local pode ser ignorada e que c = d, como visto na Figura 1.
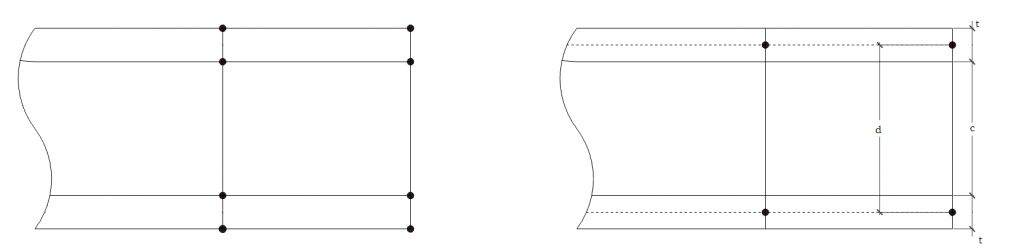
A Figura 1 também apresenta duas maneiras de se modelar painéissandwich. A primeira é utilizando elementos sólidos tanto as faces quanto no núcleo e a segunda é modelar as faces com elementos de casca e o núcleo com elementos sólidos. Em sua forma mais simples, elementos sólidos apresentam 8 nós, enquanto elementos de casca apresentam 4.
Ao se utilizar apenas elementos sólidos, as faces e o núcleo terão suas espessuras reais. O problema dessa abordagem é que elementos sólidos apresentam melhores resultados quando são cúbicos, o que obriga o usuário a subdividir o problema em muitas partes, aumentando o número de nós do modelo e, por consequência, o número de graus de liberdade. Dependendo do que se está modelando, o uso dessa abordagem tornará o tempo de processamento inaceitável.
Para diminuir o número de graus de liberdade, o modelo pode ser construído utilizando elementos de casca para representar as faces e sólidos para representar o núcleo. Os nós dos elementos de casca que representam as faces devem estar afastados por uma distância igual a (c+d)/2. Isso é compatível com a hipótese de que a espessura das faces é muito menor do que a espessura do núcleo, mas causa uma diminuição na rigidez ao cisalhamento do núcleo por conta do aumento de sua espessura em (d-c)/2. Para corrigir isso, deve-se compensar o valor do módulo de cisalhamento da seguinte forma:
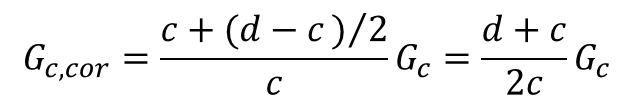
Onde Gc é o módulo de cisalhamento original do núcleo. A rigidez à tensão, por sua vez, aumentará com o aumento da espessura e portanto deve ser corrigida da seguinte forma:
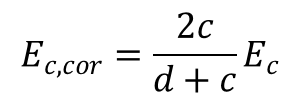
Onde Ec é o módulo de tração original do núcleo. Na realidade, o módulo de elasticidade do núcleo possui uma influência muito pequena na deflexão de uma estrutura sandwich.

Com as propriedades do núcleo corrigidas, as propriedades mecânicas das faces podem ser calculadas por meio da micromecânica ou por testes mecânicos de um laminado fabricado sob as mesmas condições do painel que se deseja simular. Definindo as condições de contorno das faces e a carga no painel, pode-se utilizar o método de elementos finitos para analisar uma estrutura sandwich.



Fernando Lopes disse:
Qual a diferença entre deformação e deflexão?
Barracuda Composites disse:
Olá, Fernando
A única diferença é que deformação é a razão entre o comprimento final e o comprimento inicial antes da aplicação da carga, enquanto deflexão é o deslocamento expresso em mm, ou qualquer outra unidade de distância. Como o método de elementos finitos pressupõe pequenos deslocamentos, a deflexão normalmente é dada na ordem de alguns milímetros mesmo.
Paulo Fernandes disse:
O que é micromecânica?
Barracuda Composites disse:
Olá, Paulo
Micromecânica é uma ferramenta de projeto de estruturas em materiais compostos que utiliza uma série de hipóteses para estimar as características do laminado final com base nas propriedades dos constituintes, ou seja, da fibra e da resina. Apesar de ser uma aproximação, consegue fornecer boas estimativas para uma etapa inicial de projeto sem um alto custo de realizar ensaios mecânicos.
Laura Dias disse:
Porque o módulo de elasticidade de tração do núcleo não influencia muito na deflexão do painel sanduíche?
Barracuda Composites disse:
Oi Laura!
Porque, em teoria, as faces são responsáveis por suportar a maior parte desse tipo de esforço. O núcleo trabalha muito mais para suportar o cisalhamento, então é natural que o módulo de cisalhamento – que pode ser interpretado com a resistência ao deslocamento por esse fenômeno – tenha uma influência muito maior.
Gustavo Renan disse:
Como definir as condições de contorno e a carga que atua nos painéis do fundo de uma embarcação que eu quero realizar a análise por elementos finitos?
Barracuda Composites disse:
Oi Gustavo,
Essa é uma tarefa complexa. As pressões que atuam no fundo da embarcação variam em função do seu arranjo estrutural, do estado de mar, na velocidade de navegação e nas acelerações que atuam no casco. As condições de contorno não são completamente conhecidas, não é possível afirmar se os reforçadores estão apoiados ou engastados e normalmente se usa uma condição intermediária entre essas duas situações. Essa é uma das vantagens do método de elementos finitos, que permite analisar várias condições conforme o amadurecimento do entendimento da situação em que a navegação ocorre.